历史编辑
大约在公元前480年,古巴比伦人和中国人已经使用配方法求得了二次方程的正根,但是并没有提出通用的求解方法。公元前300年左右,欧几里得提出了一种更抽象的几何方法求解二次方程。
7世纪印度的婆罗摩笈多是第一位懂得用使用代数方程的人,它同时容许有正负数的根。[b]
11世纪阿拉伯的花拉子米独立地发展了一套公式以求方程的正数解。亚伯拉罕·巴希亚(亦以拉丁文名字萨瓦索达著称)在他的著作Liber embadorum,首次将完整的一元二次方程解法传入欧洲。[c]
根编辑
二次方程  的两个根为:
的两个根为:

 和
和 。则点
。则点 和
和 就是二次函数与
就是二次函数与 轴的交点。根的类型如下:
轴的交点。根的类型如下:- 设
 為一元二次方程式的判別式,又記作D。
為一元二次方程式的判別式,又記作D。 - 當
 ,则方程有两个不相等的根,也即与
,则方程有两个不相等的根,也即与 轴有两个不重疊的交点,因为
轴有两个不重疊的交点,因为 是正数。
是正数。 - 當
 ,则方程有两个相等的根,也即与
,则方程有两个相等的根,也即与 轴有一个切点,因为
轴有一个切点,因为 是零。
是零。 - 當
 ,则方程没有實數根,也即与
,则方程没有實數根,也即与  轴没有交点,因为
轴没有交点,因为 是共軛複數。
是共軛複數。
设 和
和 ,我们可以把
,我们可以把 因式分解为
因式分解为 。
。
二次函数的形式编辑
二次函数可以表示成以下三种形式:
 称为一般形式或多项式形式。
称为一般形式或多项式形式。 称为因子形式或交点式,其中
称为因子形式或交点式,其中 和
和 是二次方程的两个根,
是二次方程的两个根, ,
, 是抛物线与
是抛物线与 轴的两个交点。
轴的两个交点。 称为标准形式或顶点形式,
称为标准形式或顶点形式, 即為此二次函數的頂點。
即為此二次函數的頂點。
把一般形式转换成因子形式时,我们需要用求根公式来算出两个根 和
和 ,或是利用十字交乘法(適用於有理數)。把一般形式转换成标准形式时,我们需要用配方法。把因子形式转换成一般形式时,我们需要把两个因式相乘并展开。把因子形式轉換成標準形式有特殊的方法。
,或是利用十字交乘法(適用於有理數)。把一般形式转换成标准形式时,我们需要用配方法。把因子形式转换成一般形式时,我们需要把两个因式相乘并展开。把因子形式轉換成標準形式有特殊的方法。
 代表了二次函數的對稱軸,因此兩根的平均數即為
代表了二次函數的對稱軸,因此兩根的平均數即為
 展開後比較後可得
展開後比較後可得 
不通過 和
和 求
求 及
及 公式:
公式:

 (也作
(也作 )
)
而在三種形式中皆出現的 為此二次函數的領導係數,決定二次函數圖像開口的大小與方向。
為此二次函數的領導係數,決定二次函數圖像開口的大小與方向。
图像编辑









- 系数
 控制了二次函数从顶点的增长(或下降)速度,即二次函数开口方向和大小。
控制了二次函数从顶点的增长(或下降)速度,即二次函数开口方向和大小。 越大,开口越小,函数就增长得越快。
越大,开口越小,函数就增长得越快。 - 系数
 和
和 控制了抛物线的对称轴(以及顶点的
控制了抛物线的对称轴(以及顶点的 坐标)。
坐标)。 - 系数
 控制了抛物线穿过
控制了抛物线穿过 轴时的倾斜度(导数)。
轴时的倾斜度(导数)。 - 系数
 控制了抛物线最低点或最高点的高度,它是抛物线与
控制了抛物线最低点或最高点的高度,它是抛物线与 轴的交点。
轴的交点。
| 函数 | 图像 | 函数变化 | 对称轴 | 开口方向 | 最大(小)值 |
|---|
 |  |  | 当 时, 时, 随 随 的增大而增大; 的增大而增大;
当 时, 时, 随 随 的减小而增大 的减小而增大 |  轴 轴
或 | 向上 |  |
 |  |  | 当 时, 时, 随 随 的增大而减小; 的增大而减小;
当 时, 时, 随 随 的减小而减小 的减小而减小 |  轴 轴
或 | 向下 |  |
 |  | 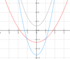 | 当 时, 时, 随 随 的增大而增大; 的增大而增大;
当 时, 时, 随 随 的减小而增大 的减小而增大 |  轴 轴
或 | 向上 |  |
 |  |  | 当 时, 时, 随 随 的增大而减小; 的增大而减小;
当 时, 时, 随 随 的减小而减小 的减小而减小 |  轴 轴
或  | 向下 |  |
 |  | 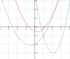 | 当 时, 时, 随 随 的增大而增大; 的增大而增大;
当 时, 时, 随 随 的减小而增大 的减小而增大 |  | 向上 |  |
 |  | 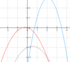 | 当 时, 时, 随 随 的增大而减小; 的增大而减小;
当 时, 时, 随 随 的减小而减小 的减小而减小 |  | 向下 |  |
x 截距编辑
当函数与 轴有两个交点时,设这两个交点分别为
轴有两个交点时,设这两个交点分别为  ,由根与系数的关系得出[d]:
,由根与系数的关系得出[d]: 和
和

顶点编辑
抛物线的顶点是它转弯的地方,也称为驻点。如果二次函数是标准形式,则顶点为 。用配方法,可以把一般形式
。用配方法,可以把一般形式 化为:
化为:

因此在一般形式中,抛物线的顶点是:

 ,则两个根的平均数
,则两个根的平均数
 坐标,因此顶点位于
坐标,因此顶点位于
 时,顶点也是最大值;
时,顶点也是最大值; 时,则是最小值。
时,则是最小值。经过顶点的竖直线

最大值和最小值编辑
導數法编辑
函数的最大值和最小值总是在驻点(又称临界点,稳定点)取得。以下的方法是用导数法来推导相同的事实,这种方法的好处是适用于更一般的函数。
设有函数 ,寻找它的極值时,我们必须先求出它的导数:
,寻找它的極值时,我们必须先求出它的导数:

 的根:
的根:
 是
是 的
的 值。现在,为了求出
值。现在,为了求出 ,我们把
,我们把 代入
代入  :
:

配方法编辑

由於實數的二次方皆大於等於0,因此當 時,
時, 有最大或最小值
有最大或最小值 。
。
二次函数的平方根编辑
二元二次函数编辑
二元二次函数是以下形式的二次多项式:

 设为零,则描述了曲面与平面
设为零,则描述了曲面与平面 的交线,它是一条圆锥曲线。
的交线,它是一条圆锥曲线。最小值/最大值编辑
如果 ,则函数没有最大值或最小值,其图像是双曲抛物面。
,则函数没有最大值或最小值,其图像是双曲抛物面。
如果  ,则当
,则当 时函数具有最小值,当
时函数具有最小值,当 具有最大值。其图像是椭圆抛物面。
具有最大值。其图像是椭圆抛物面。
二元二次函数的最大值或最小值在点  取得,其中:
取得,其中:


 且
且 ,则函数没有最大值或最小值,其图像是抛物柱面。
,则函数没有最大值或最小值,其图像是抛物柱面。如果 且
且 ,则函数在一条直线上取得最大值/最小值。当
,则函数在一条直线上取得最大值/最小值。当 时取得最大值,
时取得最大值, 时取得最小值。其图像也是抛物柱面。
时取得最小值。其图像也是抛物柱面。
註釋编辑
参考资料编辑
參見编辑
外部連結编辑
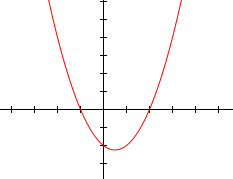


 和
和 。则点
。则点 和
和 就是二次函数与
就是二次函数与 轴的交点。根的类型如下:
轴的交点。根的类型如下:為一元二次方程式的判別式,又記作D。
,则方程有两个不相等的根,也即与
轴有两个不重疊的交点,因为
是正数。
,则方程有两个相等的根,也即与
轴有一个切点,因为
是零。
,则方程没有實數根,也即与
轴没有交点,因为
是共軛複數。




称为一般形式或多项式形式。
称为因子形式或交点式,其中
和
是二次方程的两个根,
,
是抛物线与
轴的两个交点。
称为标准形式或顶点形式,
即為此二次函數的頂點。




展開後比較後可得




(也作
)










控制了二次函数从顶点的增长(或下降)速度,即二次函数开口方向和大小。
越大,开口越小,函数就增长得越快。
和
控制了抛物线的对称轴(以及顶点的
坐标)。
控制了抛物线穿过
轴时的倾斜度(导数)。
控制了抛物线最低点或最高点的高度,它是抛物线与
轴的交点。








 ,则两个根的平均数
,则两个根的平均数
 坐标,因此顶点位于
坐标,因此顶点位于
 时,顶点也是最大值;
时,顶点也是最大值; 时,则是最小值。
时,则是最小值。

 的根:
的根:
 是
是 的
的 值。现在,为了求出
值。现在,为了求出 ,我们把
,我们把 代入
代入  :
:












 设为零,则描述了曲面与平面
设为零,则描述了曲面与平面 的交线,它是一条圆锥曲线。
的交线,它是一条圆锥曲线。






 且
且 ,则函数没有最大值或最小值,其图像是抛物柱面。
,则函数没有最大值或最小值,其图像是抛物柱面。


























